How to Recover a Bitcoin Passphrase
How I recovered a Bitcoin passphrase by performing a Breadth-First search on typos of increasing Damerau-Levenshtein distances from an initial guess.

Table of Contents
Abstract
In this post I recover a Bitcoin passphrase by performing a Breadth-First search on typos of increasing Damerau-Levenshtein distances from an initial guess. This order was chosen because the Damerau-Levenshtein distances in typos follow a Zipf distribution, so the most likely typos will be tested first. This improves on (but does not replace) BTCRecover, which has a limited definition of a typo. The code is simple to read and modify, and is available on GitHub.
Intro
The promise of Bitcoin is a hard, open source, permissionless money, but outsourcing control of your keys (e.g. to an exchange) dilutes that benefit, leaving you vulnerable to hacks[1], exit scams, and having your account frozen[2].
The mantra "not your keys, not your Bitcoin" warns us to take custody of our coins, but applies even more-so to keys that you already control: an estimated 20% of Bitcoin has been lost, while 8% has been stolen.
I learned this the hard way.
In late 2020, Ledger's software forced me to update my firmware and restore the keys from a backup[3]. After re-entering my mnemonic and passphrase into the updated device I found that I could no longer sign transactions. Fuck.
After months of poor sleep and ambient anxiety I was recently able to write a program to recover my keys. I have seen several people with the similar issues on Reddit, so I decided to write this up and provide the code. I hope it helps!
What Happened?
Bitcoin's UX is improving rapidly, but it is still very early, and there are literally infinite ways things can go wrong. Was the mnemonic incorrect? What about the passphrase? Was I using the correct key derivation path? Was there a bug in the derivation? Maybe a bug in how HWI reported the master key?
It is wise to focus on the hypotheses that make the fewest assumptions. Since it was impossible to check Ledger's code (tip: prefer Open Source), and the mnemonic was successfully restoring the passphrase-less wallet, the most likely culprit was the passphrase - or rather, I probably entered it incorrectly during the initial setup. Let's try to work out what I typed instead...
Generating Typos
Naturally, I'm not the first person that wanted to crack a Bitcoin passphrase by guessing typos. BTCRecover is a highly customisable tool for cracking mnemonics and passphrases by generating typos, but is limited in some ways.
To see why, let's take a context-agnostic look at what a typo is.
Damerau-Levenshtein Distance
The Damerau-Levenshtein Distance (sometimes just "edit distance") is a popular metric that counts the fewest number of "edits" to convert a string \(a\) to a string \(b\). Edits include:
- Inserting a character.
- Deleting a character.
- Substituting one character for another.
- Transposing two adjacent characters.
Any two strings \(a\) and \(b\) will have a sequence of edits between them. In fact, such a path could also be made with just insertions and deletions, but substitution and transposition are (probably?) counted as single edits due to how common they are. Hence, Damerau-Levenshtein space contains all possible results, including more complex speech errors like malapropisms (word-level substitution).
BTCRecover does not include insertions, hence over-prunes the search-space.
Using the above definition, let's write some Python functions to help us generate these:
def damerau_levenshtein_edits(s: str, alphabet: str):
yield from insertions(s, alphabet)
yield from substitutions(s, alphabet)
yield from deletions(s)
yield from transpositions(s)
def insertions(s: str, alphabet: str):
return (concatenate(s[:i], x, s[i:])
for i in range(len(s) + 1)
for x in alphabet)
def substitutions(s: str, alphabet: str):
return (concatenate(s[:i], x, s[i + 1:])
for i in range(len(s))
for x in alphabet)
def deletions(s: str):
return (concatenate(s[:i], s[i + 1:])
for i in range(len(s)))
def transpositions(s: str):
return (concatenate(s[:i], s[i + 1], s[i], s[i + 2:])
for i in range(len(s) - 1))
def concatenate(*args: Iterable[str]):
return "".join(args)
Breadth-First Enumeration
In the paper that introduced this measure it was found that 80% of typos have an edit distance of just 1! To verify this I plotted the edit distance for all English typos in this GitHub Typo Corpus (code):
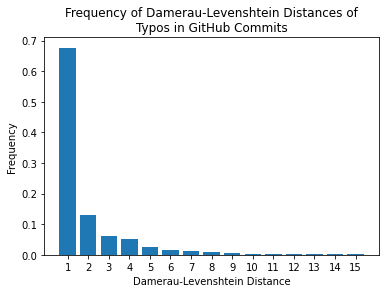
Close enough! More importantly, it follows a Zipf distribution (i.e. a discrete Pareto distribution), which occurs in natural language all the time. This means we can rapidly converge on the correct answer by enumerating strings in ascending order of Damerau-Levenshtein distance. The dataset also contains malapropisms, so even complex errors occur more frequently within short edit distances.
This order will naturally occur if we define an (implicit) graph of strings where each edge represents a single edit, and perform a Breadth-First traversal (as the nearest neighbors will be explored first). If I had further worked out character-level probabilities for each typo, we could probably use Dijkstra's Algorithm to further speed things up, and as Reddit user Quantris mentions, for a long initial string we might wish to use Iterative-Deepening Depth-First Search to reduce memory usage.
Here's an iterator to perform the traversal:
def all_typos(root: str, alphabet: str):
neighbors = lambda x: damerau_levenshtein_edits(x, alphabet)
discovered = {root}
frontier = deque([(0, root)])
while frontier:
distance, current = frontier.popleft()
yield {"distance": distance, "typo": current}
for neighbor in neighbors(current):
if neighbor not in discovered:
frontier.append((distance+1, neighbor))
discovered.add(neighbor)
The above loop will never terminate - it is up to the caller to cease iteration when appropriate.
Terminating Conditions
Since we don't know what string we are looking for we will need to use each passphrase attempt to derive one of the following:
- The master public key or fingerprint.
- Any account public keys or fingerprints.
- A receiving or change address.
- A transaction IDs (we can fetch the addresses involved from the mempool).
- A database of used addresses if none of the above are known.
Anything under the master key (such as an account key or address) require guessing the correct derivation path. While there are infinite possibilities[4], there are only finite wallet implementations, so this list of the different derivation paths used in wallets may come in handy. I had the master fingerprint so didn't need any derivation paths.
Here is code using bip_utils to derive the fingerprint from a mnemonic and passphrase:
from bip_utils import Bip32, Bip39SeedGenerator
def fingerprint(mnemonic: str, passphrase: str):
seed_bytes = Bip39SeedGenerator(mnemonic).Generate(passphrase)
master = Bip32.FromSeed(seed_bytes)
return master.FingerPrint()
def crack(
mnemonic: str,
master_fingerprint: str,
passphrase_guess: str,
alphabet: str,
):
binary_fingerprint = binascii.unhexlify(master_fingerprint)
passphrase_typos = all_typos(passphrase_guess, alphabet)
for typo in passphrase_typos:
if fingerprint(mnemonic, typo["typo"]) == binary_fingerprint:
return typo
Search Party 🎉
Below I have included code for how to use the above functions to crack my wallet.
# crack.py
from string import ascii_lowercase
ALPHABET = ascii_lowercase
MASTER_FINGERPRINT = b"6aa00e9a"
GUESS = "hysterichorsebatterystaple"
MNEMONIC = """
chase wonder voice rack
custom sport fix decline
body hollow wreck stay
dress resist space solid
gospel pumpkin shoot tank
cable dignity own pigeon
""".strip().split()
if __name__ == "__main__":
result = crack(" ".join(MNEMONIC), MASTER_FINGERPRINT, GUESS, ALPHABET)
print(f"{result['typo']} found at distance {result['distance']}")
And the big reveal (run this on an offline computer to avoid loss of funds):
$ python crack.py
historichorsebatterystaple found at distance 2
This completed in 165 minutes (close to 3 hours), which isn't bad at all considering by this stage we had already checked the vast majority of likely typos.
It turns out I had mistyped "historic" instead of "hysteric". This made me laugh, since I remember doing my best to not type "hysteria" (which I couldn't stop thinking about, because of its messed up history). I guess focusing too hard on that final "c" caused me to be lax with the rest.
If you don't have a clue of what your passphrase is, try this list of common passwords - humans are more similar than we realise.
Prevention
Although it wasn't too hard for me to fix in the end, I could have done without the hassle. To avoid this happening in the first place:
- Test your backups - Although wallets usually prompt you to re-enter/re-read things, your backup is only guaranteed after you actually use it. The best way to do this is to use Ian Coleman's Tool offline in Tails, or another device (in case your wallet has bugs).
- Use multi-sig - In theory, adding a passphrase can protect you from say, a $5 wrench attack. In practice it introduces an additional single point of failure. A multi-sig setup (e.g. 2-of-3) adds redundancy, and uses mnemonics instead (which have some built in error correction). The tooling has improved to the point where this is really easy (and free if you use paper wallets). I'll write a guide on this someday, but Michael Flaxman has a good guide here.
Conclusion
In this post I demonstrated that a Breadth-First search in ascending order of Damerau-Levenshtein distances is a practical method to recover a Bitcoin passphrase that was mistyped during an initial setup.
I hope to add support for address derivation, mnemonic correction, and improve the performance in the future. But for now it is fairly ad-hoc and specific to my situation. If you are still stuck please contact me and I'll try to help.
If this helped or entertained you sign up to my mailing list for more words!
Special thanks to nopara73 (author of Wasabi) for his help in the wallet derivation part of this code.
Of course, individual users are more likely to have insecure environments, but exchanges are much higher value targets that they are more susceptible to attack. ↩︎
This could be for illegal activity, censorship (e.g. if you sell marijuana or run an OnlyFans account), or even a simple policy change that requiring more personal information. Even a temporary freeze can be disruptive and stressful. ↩︎
I could write a long-ass post about why Ledger have dangerous UX, and maybe someday I will! But for now, if you are in the market for a hardware wallet, I'd recommend looking at the Cobo Vault (not a paid endorsement). ↩︎
The details of key derivation are outside the scope of this post. If you want to understand it in depth, I recommend Chapter 4 of Mastering Bitcoin by Andreas Antonopoulos, or this helpful flowchart by @septem_151. ↩︎
alexbowe.com Newsletter
Join the newsletter to receive the latest updates in your inbox.

